Si se trata de resolver el ejercicio conforme un grafo directo pero no se especifica un coste reverso (reverse_cost), entonces pgrouting se parará al llegar al nodo 9 y no encontrará una solución:

routing1=# select * from pgr_dijkstra ('select gid as id, source, 
   target, st_length(geom) as cost from wr', 4, 11, true);
 seq | path_seq | node | edge |       cost       |     agg_cost
-----+----------+------+------+------------------+------------------
(0 rows)

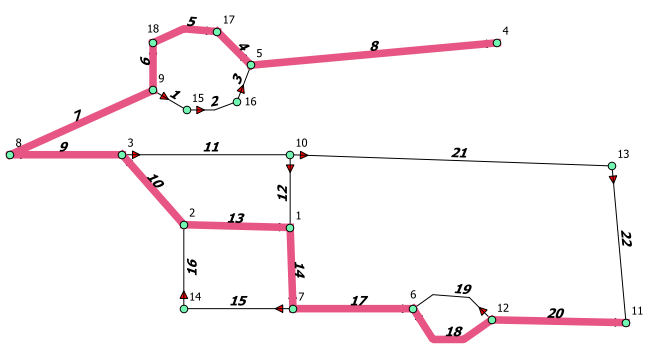
Nuestra red en realidad tiene todos los tramos de doble sentido salvo las dos rotondas. Para modelarla añadiremos dos campos, un campo cost con la longitud de cada tramo y otro reverse_cost también con la longitud de cada tramo excepto en los tramos 1, 2, 3, 4, 5, 6, 18 y 19 que son los que forman las dos rotondas.

routing1=# alter table wr add cost double precision;
routing1=# alter table wr add reverse_cost double precision;
routing1=# update wr 
         set cost = st_length(geom), reverse_cost = st_length(geom);
routing1=# update wr set reverse_cost = -1
           where gid in (1,2,3,4,5,6,18,19);

En este caso para ver el resutlado de forma gráfica, vamos además a crear una nueva tabla espacial que contendrá la ruta calculada:

routing1=# create table dijkstra1 (gid serial, vertex_id integer, 
             geom geometry (MultilineString, 0));
routing1=# insert into dijkstra1 (vertex_id, geom) 
  select wr.gid, wr.geom from 
  pgr_dijkstra 
     ('select gid as id, source, target, cost, reverse_cost from wr',
      4, 11, true)
  , 
  wr where wr.gid = edge;

En este caso se ha respetado la dirección de las rotandas incluso aunque el coste de los tramos 4, 5, 6 es mas alto que los tramos 3, 2, 1. La siguiente figura muestra la capa dijkstra1 con la ruta calculada.

Ruta más corta en grafo directo

Si la red es muy grande siempre se puede acelerar el cálculo de la ruta utilizando un filtro espacial que únicamente seleccione los tramos dentro de una caja (expandida cierta cantidad) que contenga a los nodos inicial y final.