Haz clic aquí para ver la versión en español.
I want to show you the summary of a research that we have recently published. We will only focus on the results, for the methodology details you can check the two published articles [1] [2].
As we know to perform any geospatial analysis it is necessary to use a projected coordinate reference system (CRS). The current available geospatial software implements certain operations on the ellipsoid, without using a projected SRS, such as the direct and inverse problems of geodesy, and in this way allows to calculate distances on the ellipsoid, or to calculate a point from an azimuth and a distance. But, these operations are not enough to carry out a full spatial analysis on the ellipsoid, and to address a simple intersection of two segments, or the minimum distance from a point to a line is still solved using a projected CRS, and thereforem any more complex operation such as a full geometric intersection, a buffer, etc. is calculated in the same way.
This way several issues appear:
- What projected CRS do I use to perform the calculations? This will undoubtedly limit the geographic zone of the analysis.
- And worst of all, what error am I making when using a projected CRS? And I go further, these unknown errors could be greater than the cartographic precision of my geo data?
In the articles [1] [2] two cases are studied: an intersection of two linear segments, and the minimum distance from a point to a line, but that is, considering that these lines are geodesic. Based on these two cases, it would be possible to build or improve a computational geometry library (e.g. JTS) to perform the full geo spatial analysis on the ellipsoid.
Problem to solve:
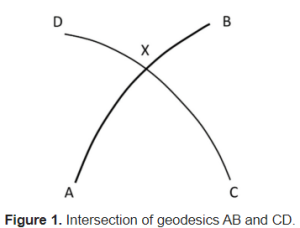
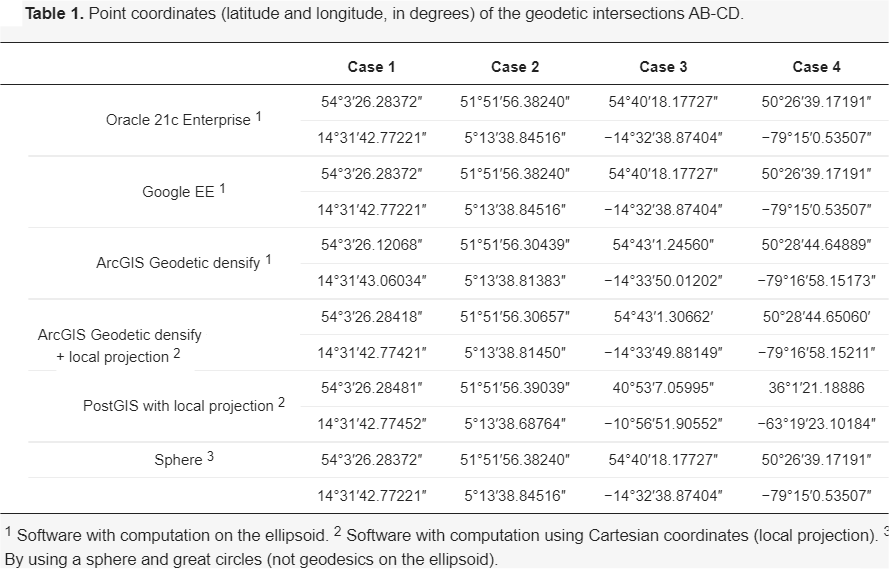
Suppose we want to obtain the intersection point of two segments AB and CD each one defined by their two initial and final points (figure 1). Thus, we consider the following table with the coordinates of four different examples:
The distance AX and CX gives us an idea of the length of these segments, from less than 10 km in case 1, up to more than 10,000 km in case 4.
Table 1 shows the intersection point (point X) calculated by some of the best-known geo spatial software on the market, some software mention that they work directly on the ellipsoid (supposedly) and others use a projected CRS for the calculation.
It is scary at first to see how each software obtains different results (point X). So what software gives the most correct results? And, what’s more, do any of them give the exact result? And if not, what error does each software make?
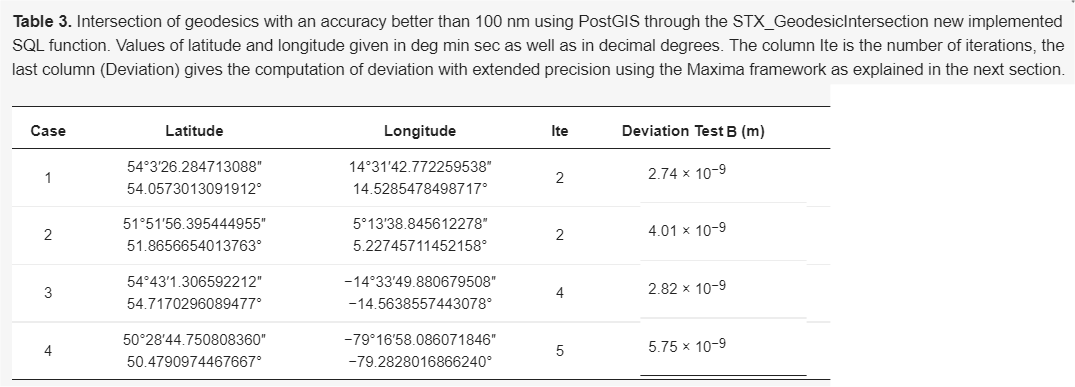
Table 3 shows the point X calculated by the algorithm proposed by the authors of this article. Specifically with the implementation made in PostGIS (STX_GeodesicIntersection function), although any other implementation should give the same results.
As you can see, it is a fast convergence algorithm (see number of iterations). Furthermore, Test B (see article [1] for its definition) calculates the distance from the exact point X to the calculated point. An error of less than 100nm indicates that computational precision has been achieved (calculations with 64-bit floating types).
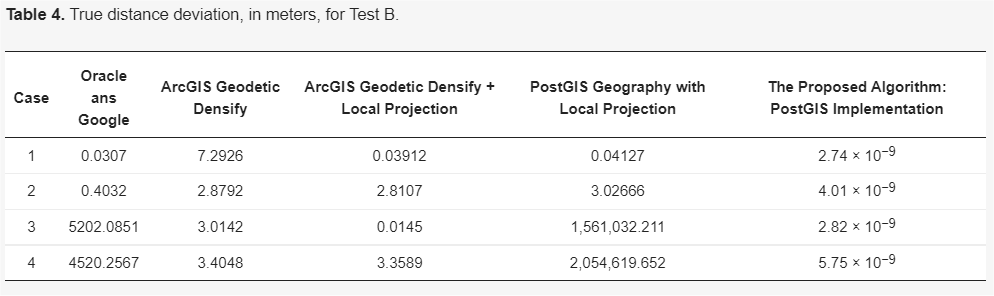
And as a final result, we present the table with the errors made by the different software.
See as in case 2 with geodesics of only a few tens of km in length, applications such as PostGIS, ArcGIS, etc. make about 3m of error.
The PostGIS and Java test implementation can be downloaded from [3].
Finally, mention that, in a normal computer, about 20,000 intersections per second have been obtained. Perhaps, now is the time to migrate certain geospatial libraries such as JTS (GEOS), GDAL, etc. so that they carry out the calculations in full on the ellipsoid and thus be able to forget about the projected CRS, and leave them purely for aesthetic purposes.
[1] https://www.mdpi.com/2076-3417/11/11/5129
Martínez-Llario JC, Baselga S, Coll E. Accurate Algorithms for Spatial Operations on the Spheroid in a Spatial Database Management System. Applied Sciences. 2021; 11(11):5129. https://doi.org/10.3390/app11115129
[2] https://link.springer.com/article/10.1007/s11200-017-1020-z
Baselga, S., Martínez-Llario, J.C. Intersection and point-to-line solutions for geodesics on the ellipsoid. Stud Geophys Geod 62, 353–363 (2018). https://doi.org/10.1007/s11200-017-1020-z