Quiero mostraros el resumen de una investigación que hemos publicado recientemente. Solo nos centraremos en los resultados, para las explicaciones de la metodología podéis consultar los dos artículos publicados por nosotros [1] [2].
Como sabemos para realizar un análisis espacial completo es necesario utilizar un sistema de referencia de coordenadas (SRC) proyectado. El panorama del software actual implementa ciertas operaciones sobre el elipsoide, sin utilizar un SRS proyectado, como los problemas directo e inverso de la geodesia, y permite de esta manera calcular distancias sobre el elipsoide, o calcular un punto a partir de un azimut y una distancia. Pero, es que estas operaciones no son suficientes para realizar un análisis espacial completo sobre el elipsoide, y un problema tan sencillo como la intersección de dos segmentos lineales, o la distancia mínima de un punto a una recta se siguen resolviendo utilizando SRC proyectados, y por ende cualquier operación más compleja como una superposición de polígonos, intersección de capas lineales, un área de influencia, etc. se calcula de la misma manera.
Aparecen así varios problemas:
- ¿Qué SRC proyectado utilizo para realizar los cálculos?, lo cual sin duda limitará la extensión geográfica del análisis.
- Y lo peor, ¿qué errores estoy cometiendo al utilizar un SRC proyectado? Y voy más allá, ¿estos errores (que no los conozco) podrían ser superior a la precisión cartográfica de mis datos?
En los artículos [1] [2] se estudian dos casos: una intersección de dos segmentos lineales, y la mínima distancia de un punto a una línea, pero eso sí considerando que esas líneas son geodésicas. Apoyándose en estos dos casos sería posible construir o mejorar una biblioteca de geometría computacional (e. g. JTS) para que fuera capaz de calcular un análisis espacial completo sobre el elipsoide.
Problema a resolver:
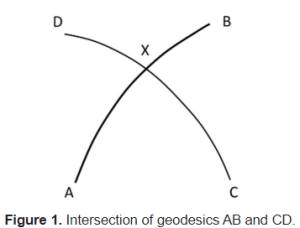
Supongamos que queremos obtener el punto de intersección de dos segmentos AB y CD definidos cada uno por sus dos puntos inicial y final (figura 1). Así, consideramos el siguiente cuadro con las coordenadas de cuatro ejemplos diferentes:
La distancia AX y CX nos da una idea de la longitud de dichos segmentos, de menos de 10 km en el ejemplo 1, hasta más de 10000 km en el ejemplo 4.
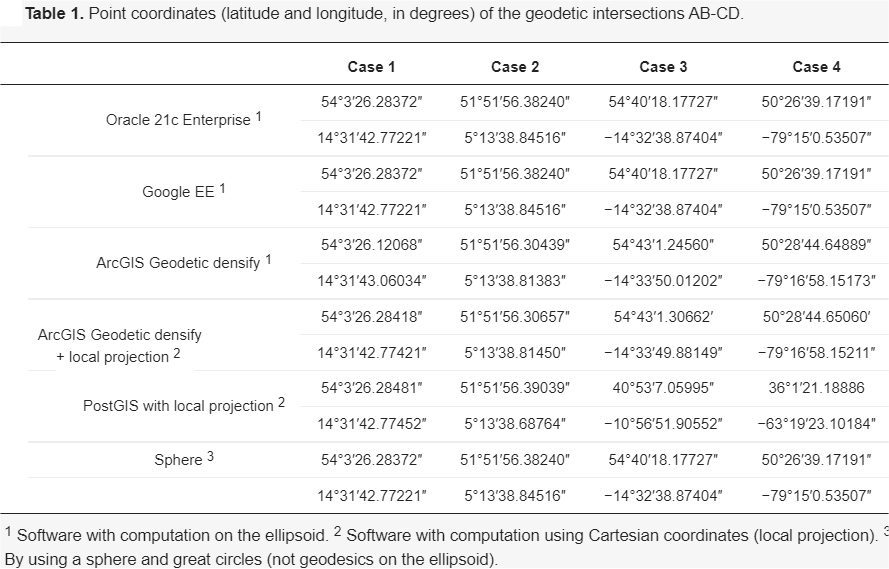
La tabla 1, muestra el punto de intersección (punto X) calculado por algunos de los aplicativos y bases de datos espaciales más conocidas del mercado, algunos softwares mencionan que trabajan directamente en el elipsoide (supuestamente) y otros utilizan un SRC proyectado para el cálculo.
Asusta en un primer momento ver como cada software obtiene diferentes resultados (punto X). Entonces, qué ¿software da los resultados más correctos? Y, es más, ¿alguno de ellos da el resultado exacto?, y si no es así ¿qué error comete cada software?
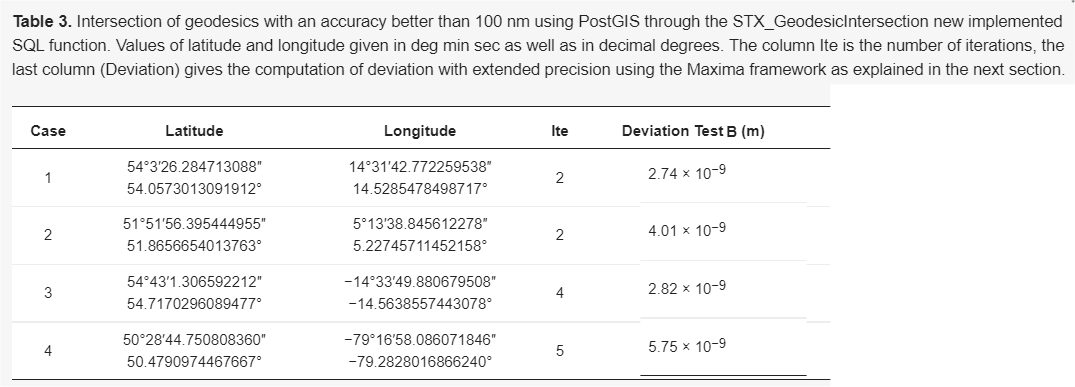
La tabla 3, muestra el punto X calculado por el algoritmo propuesto por los autores de este artículo. En concreto con la implementación realizada en PostGIS (función STX_GeodesicIntersection), aunque cualquier otra implementación debe dar los mismos resultados.
Como se puede ver es un algoritmo de rápida convergencia (ver número de iteraciones). Además, el Test B (ver artículo [1] para su definición) calcula la distancia del punto exacto X al punto calculado. El error inferior a 100nm indica que se ha llegado a alcanzar la precisión computacional (cálculos con tipos flotantes de 64 bits).
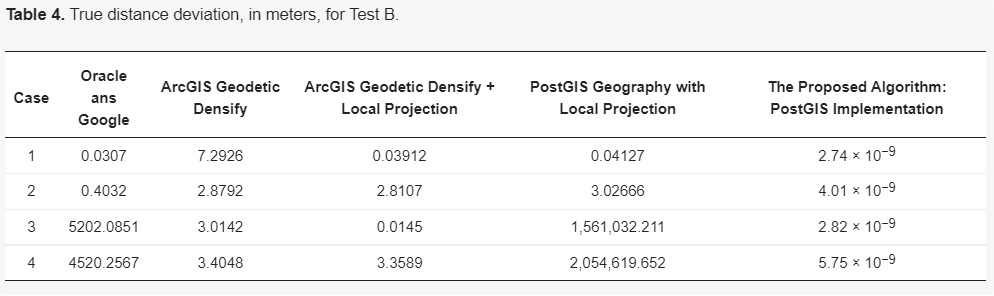
Y como resultado final, presentamos la tabla con los errores cometidos por los diferentes aplicativos.
Ver como en el caso 2 con geodésicas de solo algunas decenas de km de longitud, aplicativos como PostGIS, ArcGIS, etc. comenten alrededor de 3m de error.
La implementación de prueba realizada en PostGIS y Java se puede descargar desde [3].
Por último, mencionar que, en un ordenador normal, se han obtenido unas 20000 intersecciones por segundo. Quizás, sea el momento ya, de migrar ciertas librerías geoespaciales como JTS (GEOS), GDAL, etc. para que realicen los cálculos de forma íntegra sobre el elipsoide y así poder olvidarnos de los SRC proyectados, y dejarlos meramente para fines estéticos.
[1] https://www.mdpi.com/2076-3417/11/11/5129
Martínez-Llario JC, Baselga S, Coll E. Accurate Algorithms for Spatial Operations on the Spheroid in a Spatial Database Management System. Applied Sciences. 2021; 11(11):5129. https://doi.org/10.3390/app11115129
[2] https://link.springer.com/article/10.1007/s11200-017-1020-z
Baselga, S., Martínez-Llario, J.C. Intersection and point-to-line solutions for geodesics on the ellipsoid. Stud Geophys Geod 62, 353–363 (2018). https://doi.org/10.1007/s11200-017-1020-z