En esta serie de artículos sobre Pgrouting muestro el funcionamiento básico de esta biblioteca de rutas que trabaja sobre PostGIS.

Trato de actualizar el capítulo F.11 del libro de PostGIS, que al utilizar la versión anterior de pgrouting se ha quedado obsoleto.

Este material ha sido realizado por José Carlos Martínez y se publica mediante licencia Creative Commons

Dijkstra

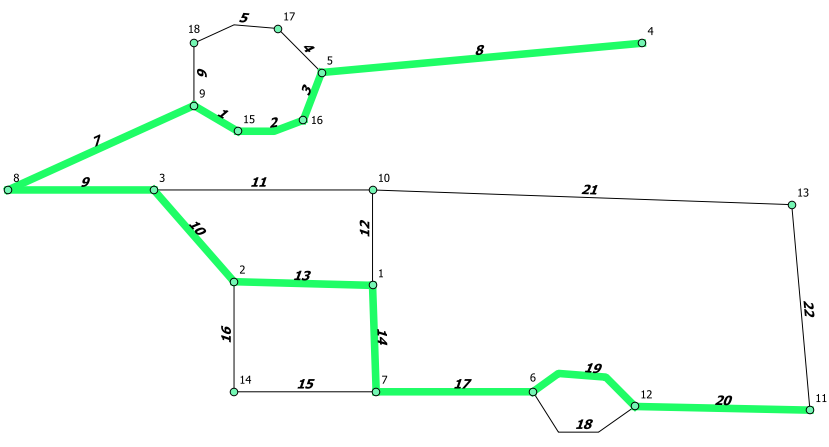
Como primer ejemplo se va a calcular el camino más corto desde el nodo 10 al nodo 17 utilizando el algoritmo de Dijkstra que nos asegura la mejor ruta posible. Vamos a considerar todos los tramos de doble dirección (grafo indirecto) y el coste va a consistir en la longitud de cada tramo.

Ruta más corta en grafo indirecto

La función a utilizar se llama shortest_path y tiene una firma similar a la siguiente:

CREATE OR REPLACE FUNCTION pgr_dijkstra(
edges_sql text,
start_vid integer,                                          
end_vid integer,
directed boolean, -- por defecto si no se especifica es true
) RETURNS SETOF (seq, path_seq, node, edge, cost, agg_cost)

Argumentos:

• edges_sql: Se corresponde con una consulta que pgrouting ejecutará para obtener los datos de la red. Esta consulta Select debe de devolver los siguientes campos (no es necesario que estén en orden, aunque hay que respetar el nombre y el tipo de datos).
• id: Any-Integer -> Identifica el número de eje/tramo de la red.
• source: Any-Integer -> Identifica el número de nodo inicial del tramo.
• target: Any-Integer -> Identifica el número de nodo final del tramo.
• cost: Any-Numerical (ej.: Double precisión) -> Coste del tramo necesario para atravesarlo en la dirección del nodo inicial al nodo final.
• reverse_cost: Any-Numerical (opcional) -> Coste del tramo necesario para atravesarlo en la dirección del nodo final al nodo inicial. Únicamente se necesita si el grafo se ha definido directo y el argumento directed es true.

 Any-Integer hace referencia a cualquier entero, ej.: Integer, BigInt, etc. Any-Numerical hace referencia a cualquier tipo decimal, ej.: Double precisión, Real, Integer, etc.

• start_vid: Número de nodo origen de la ruta a calcular.
• end_vid: Número de nodo final de la ruta a calcular.
• directed: true (el grafo es directo) o false (el grafo es indirecto). En el caso de grafo directo se utilizará el campo reverse_cost de la consulta SQL del primer argumento (edges_sql) como coste para atravesar el tramo en dirección opuesta.

Como salida la función devuelve el conjunto de filas conteniendo la ruta calculada, cada fila tiene los siguientes campos:

• seq: Valor secuencial empezando en 1
• path_seq: Posición relativa respecto al inicio de la ruta. El valor 1 representa el inicio.
• [start_vid]: Identifica el número de nodo inicial del tramo de la ruta. Solo aparece cuando se utiliza la variedad del algoritmo que permite varios vértices de salida.
• [end_vid]: Identifica el número de nodo final del tramo de la ruta. Solo aparece cuando se utiliza la variedad del algoritmo que permite varios vértices de llegada.
• node: Número de nodo en la ruta, desde start_vid hasta end_vid.
• edge: Identifica el eje del tramo de la ruta. Toma el valor -1 para el último eje.
• cost: Coste del tramo.
• agg_cost: Coste total acumulado desde el tramo inicial

routing1=# select * from pgr_dijkstra ('select gid as id, source, 
  target, st_length(geom) as cost from wr', 4, 11, false);
 seq | path_seq | node | edge |       cost       |     agg_cost
-----+----------+------+------+------------------+------------------
   1 |        1 |    4 |    8 | 88.3628881374981 |                0
   2 |        2 |    5 |    3 | 13.9283882771841 | 88.3628881374981
   3 |        3 |   16 |    2 | 18.5440037453175 | 102.291276414682
   4 |        4 |   15 |    1 | 13.8924439894498 |     120.83528016
   5 |        5 |    9 |    7 | 55.9464029227975 |  134.72772414945
   6 |        6 |    8 |    9 |               40 | 190.674127072247
   7 |        7 |    3 |   10 | 33.3016516106934 | 230.674127072247
   8 |        8 |    2 |   13 | 38.0131556174964 |  263.97577868294
   9 |        9 |    1 |   14 | 29.0172362570938 | 301.988934300437
  10 |       10 |    7 |   17 |               43 | 331.006170557531
  11 |       11 |    6 |   19 | 32.9544385764327 | 374.006170557531
  12 |       12 |   12 |   20 | 48.0104155366312 | 406.960609133963
  13 |       13 |   11 |   -1 |                0 | 454.971024670595

Como se puede observar la ruta trazada atraviesa algunos ejes y las rotondas en dirección contraria a la establecida por los nodos inicial y final (flechas de la figura).